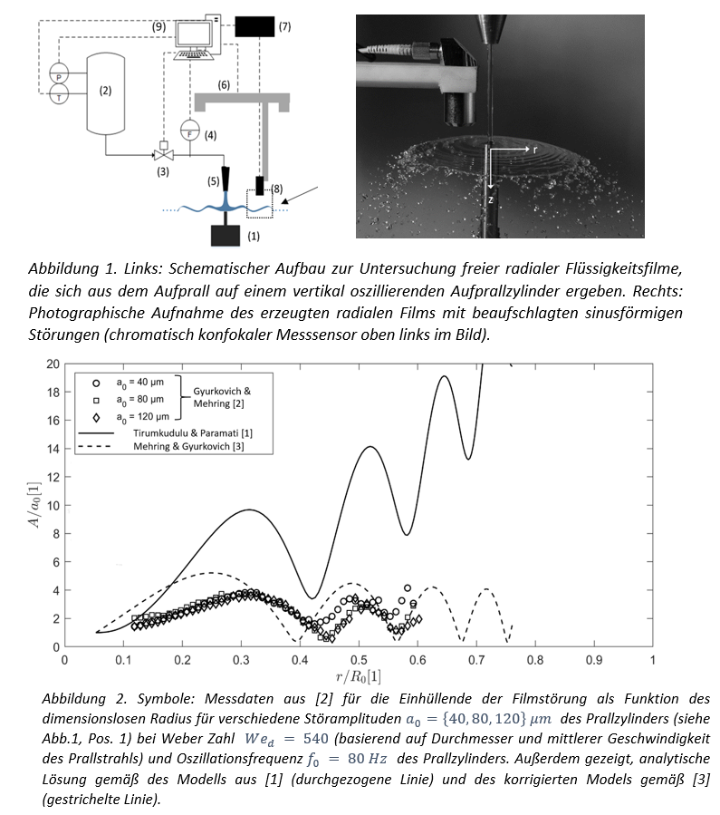
Im Rahmen der experimentellen Untersuchung freier Flüssigkeitsfilme mittels der sog. chromatisch konfokalen Messtechnik wurden die Forscher des Instituts für Mechanische Verfahrenstechnik der Universität Stuttgart auf eine vor 10 Jahren am Indian Institute of Technology (IIT) auf analytischem Wege nachgewiesenen Instabilität an freien, sinusförmig angeregten und sich radial ausbreitenden Flüssigkeitsfilmen aufmerksam [1]. Diese vermeintlich „neu entdeckte“ Instabilität begründete sich, im Gegensatz zu der für radiale Filme bereits bekannten kapillarkraftbedingten Instabilität (dokumentiert von G. I. Taylor im Jahr 1959) auf Impulsterme höherer Ordnung, welche infolge der Ausdünnung des Films in radiale Richtung in den linearisierten Erhaltungsgleichungen auftreten. Da trotz umfangreicher und intensiver experimenteller Untersuchungen (siehe Abb. 1), das genannte instabile Verhalten infolge Filmausdünnung nicht nachgewiesen werden konnte [2], wurde die vom IIT publizierte Störreihenentwicklung im Detail überprüft und erneut durchgeführt. Es konnte dabei gezeigt werden, dass das ursprüngliche Lösungsvorgehen inkonsistent war. Letztendlich ergab die korrekte und konsistente Herleitung der linearen Störgleichungen 2ter Ordnung für den sich radial ausbreitenden und sinusförmig angeregten Film, dass eine (impulsbedingte) Instabilität infolge der Filmausdünnung nicht existiert [3] (siehe Abb. 2). Damit müssen vorherige Arbeiten, welche sich auf die zuvor beschriebene und aufgrund der Filmausdünnung vorhergesagten Instabilität stützen neu bewertet werden.
[1] M. S. Tirumkudulu and M. Paramati, “Stability of a moving radial liquid sheet: Time-dependent equations,” Phys. Fluids 25(10), 102107 (2013).
[2] A. Gyurkovich and C. Mehring, “Measurements of sinuous waves on mechanically forced radially expanding free planar liquid sheets using chromatic confocal measurements”, Atom. Spray, 33 (6): 19-44 (2023).
[3] C. Mehring and A. Gyurkovich, “Comment on ‘Stability of a moving radial liquid sheet: Time-dependent equations’ [Phys. Fluids 25, 102107 (2013)]”, Phys. Fluids, 35, 099101 (2023).
| Datei-Anhänge |
|---|